LATEST

Manchester scientists have made a remarkable...
Thu, Apr 25th 2024In a thrilling breakthrough in the realm of...

AI software revolutionizes plant engineering to...
Wed, Apr 24th 2024At Salk in La Jolla, researchers are collaborating...
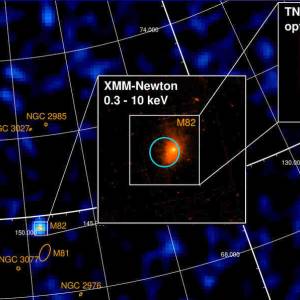
University of Geneva researches a massive magnetic...
Wed, Apr 24th 2024A groundbreaking discovery has been made by the...

Supercomputer simulations uncover the dynamics of...
Tue, Apr 23rd 2024New research conducted by a team of scientists...
AI tool predicts responses to cancer therapy using...
Thu, Apr 18th 2024A recent study conducted by researchers from...